Ya conoceis de entradas anteriores que fi = número de oro = 1,618033..., es el cociente de las dimensiones de rectángulos armoniosos o perfectos. Pero existen otros números también llamados metálicos que guardan sorprendentes propiedades y que también tienen aplicaciones en el arte. Estos números son: número de plata, número de platino, número de bronce, número de cobre, número de níquel, etc... incluso uno más moderno llamado número de plástico.
¿Qué características tienen en común estos números metálicos?
- Son números irracionales con infinitos decimales no periódicos
- Son límites de sucesiones tipo Fibonacci
- Se pueden descomponer en fracciones continuas
- Son soluciones de ecuaciones de segundo grado (salvo el número de plástico, que lo es de una ecuación de grado 3, por eso no se le considera metálico)
- Están presentes en la Naturaleza y/o arte, arquitectura, etc...
EL NÚMERO DE ORO
Viene de resolver la ecuación x^2-x-1=0, cuya solución positiva es x = (1+√5)/2 = 1,6180... Se puede obtener también del cociente entre un término muy grande y el término anterior de una sucesión {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,etc...} donde el término siguiente es la suma de los dos anteriores, es decir,
a(n+1) = an + a(n-1) con a
1 = a
2 =1 . Cuanto más avancemos en la sucesión el cociente se aproxima más al número de oro. Ejemplo: 89 /55 = 1,6181818... que tiene cifras iguales hasta las milésimas.
Su expresión en forma de fracción continua (no os asusteis) es la siguiente:
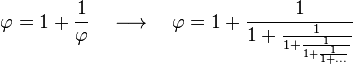EL NÚMERO DE PLATA
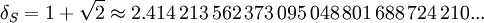
Viene de la ecuación
x^2-2x-1=0, cuya solución positiva es 1+√2 y su expresión en fracción continua es la siguiente:
Su sucesión de Fibonacci es la siguiente:
a(n+1) = 2an + a(n-1) partiendo de a
1 = a
2 =1. Entonces la sucesión de números es {1, 1, 3, 7, 17, 41, 99, 239,...) y hallando el cociente entre los últimos términos 239/99 = 2,414141414..., que está bastante próximo al valor real.
En la antigua ciudad de Ostia (Roma), arquitectos del siglo II d.C. diseñaron un conjunto de edificios a partir de un cuadrado-patrón: el llamado “cuadrado del corte sagrado” en el que se oculta el número de plata: θ= 1 + √2 = 1 + 1,4142.... = 2,4142......Al igual que el número de oro aparece en el pentágono regular, el número de plata lo hace en el octógono regular como la razón entre el lado y la diagonal. Nos lo encontramos, también, en objetos cotidianos rectangulares y principalmente en rectángulos que encierran logotipos y anuncios en la prensa escrita. La relación entre los lados de estos rectángulos es la del número de plata:1 y 1+√2 . Por eso se les llama Rectángulos de Plata.
EL NÚMERO DE PLATINO
De la misma forma que hemos presentado el número de plata, también podemos hacer lo mismo con el número de platino. De hecho, el número de platino δ
Pt= 1 + √3 = 1 + 1,7320508... = 2,7320598.... Proviene de la solución positiva de la ecuación x^2-2x-2=0.
Su sucesión de Fibonacci asociada es a
(n+1) = 2a
n + 2a
(n-1)
Sus términos son todos pares menos los iniciales: {1, 1, 4, 10, 28, 76, 104, 360, 928, 2576, 7008, 19168...}. Si cogemos estos dos últimos términos 19168/7008 = 2,735.....
Esta proporción ha sido muy utilizada en la arquitectura italiana del Renacimiento.
Otro día hablaremos del número de bronce y el número de cobre
LA LECHE SAGRADA
Como bien habeis notado, mañana 30 de enero no hay clases, se celebra el día de la Enseñanza; antes había varios días: día de los maestros, de los profesores, de los profesores de formación profesional. Sus santos o patrones respectivos son, a saber, S. José de Calasanz, Sto. Tomás de Aquino y S. Juan Bosco. Las autoridades decidieron unificar los 3 días en 1.
Las respuestas anónimas y sinceras (da igual si positivas o negativas), por favor, en los comentarios. No te quedes indiferente, opina. Tu opinión nos sirve de crítica y también para mejorar.
Con este test vas a ver qué personaje importante del mundo es tu modelo a seguir … no vale hacer trampa:
El número de Níquel proviene de la ecuación de segundo grado x^2-x-3=0, su solución positiva es 
Si os fijais, guarda relación con el de bronce, es una unidad menos. 
Siguiendo de forma análoga al número de oro y de plata, os presento los siguientes números:
Ya conoceis de entradas anteriores que fi = número de oro = 1,618033..., es el cociente de las dimensiones de rectángulos armoniosos o perfectos. Pero existen otros números también llamados metálicos que guardan sorprendentes propiedades y que también tienen aplicaciones en el arte. Estos números son: número de plata, número de platino, número de bronce, número de cobre, número de níquel, etc... incluso uno más moderno llamado número de plástico.
En este recién estrenado año 2009 se celebrará el 2º centenario del nacimiento de Charles Darwin, el científico que confirmó la teoría de la Evolución de los seres vivos en su libro más famoso "El origen de las especies", que curiosamente cumple 150 años desde su publicación. Mucha gente piensa que la evolución de los seres vivos no se ha dado nunca y otra gente ha ideado cómo será nuestro planeta y los seres vivos que lo habitarán en un futuro lejano. 
La serie en cuestión que lo aborda se llama "Futuro salvaje", la cual basándose en principios científicos y observaciones actuales de la Naturaleza nos ofrece una visión bastante creíble de cómo será el planeta Tierra dentro de 5 millones, 100 millones y 200 millones de años. Es una serie bastante interesante, que os recomiendo que veáis; se pueden sacar prestados los DVDs de muchas bibliotecas. Os dejo dos trozos del primer capítulo sobre cómo han evolucionado las gaviotas y codornices dentro de 5 millones de años. Lo siento, pero los seres humanos no estamos entre las especies supervivientes. Aunque quién sabe... Quién estará vivo para contarlo?
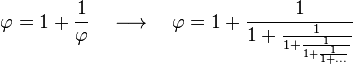
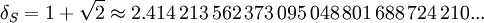
Tras la resaca de la Nochevieja me dispongo a ver las noticias. No puedo terminar el telediario si no fuera por los nacimientos de los primeros niños del 2009... En fin, les deseo un mundo feliz a éstos que han venido a nuestro planeta y por supuesto, a todos los que ya estamos en él. A vosotros todos, os quiero de vuelta el día 8 de enero. Por cierto, echo de menos vuestros comentarios.
.jpg)
