a) hacer el dibujo relacionado con el problema lo más exacto posible.
b) recordar el teorema de Pitágoras en problemas donde hay alturas, aristas, etc... o simplemente triángulos rectángulos.
c) recordar el teorema de Tales o sus propiedades derivadas. Recordar las propiedades de la semejanza de figuras y las propiedades de las proporciones.
d) recordar las fórmulas más importantes de áreas y volúmenes de figuras geométricas.
e) muchas veces hay que plantear ecuaciones de segundo grado. Repasar la resolución de ecuaciones.
EL BAMBÚ.
Un bambú de 32 codos de altura se quebró por un fuerte viento. La punta del bambú tocó el suelo a 16 codos de distancia del pie del bambú. Dime, pequeña matemática, ¿a qué altura se quebró el bambú?
EL LOTO.
En un lago había un gran número de gansos rojos y grullas. Un loto sobresalía de la superficie del agua una altura de medio codo y una brisa susurrante lo fue inclinando hasta que su punta se hundió a dos codos de distancia de donde emergía. Oh, matemática, dime rápidamente la profundidad del lago.
FIGURAS IMPOSIBLES.
Si un idiota dice que hay una cuadrilátero de lados 2, 6, 3 y 12, o un triángulo con lados 3, 6 y 9, explícale por qué no existen.
VOLÚMENES DE POLIEDROS ATÍPICOS.
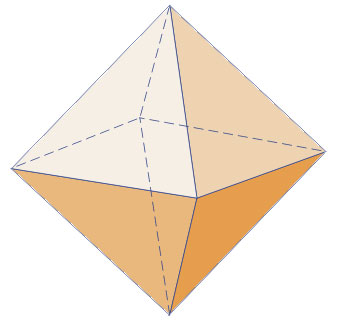
Hallar el volumen que tiene un octaedro de 10 cm de arista
Hallar el volumen de un cuboctaedro de 10 cm de arista.
Nota: un cuboctaedro es un cubo cuyos vértices (tetraedros con ángulos de 90º) han sido cortados a la mitad de la arista del cubo original. Ver figura adjunta.

.jpg)




12 comentarios:
Hola Miguel Ángel!!
Soy Luis, el hermano de Ignacio. Jajaja
Y como le he visto estar rompiendose la cabeza para hacer el del bambú, digo... voy a entrenarme yo también.
Pero resulta que no era tan complicado... jajaja
Bueno aquí va la solución:
,
,
,
,
,
,
,
. -
. -
. -
. -
. -
. -
.*******-
Este "dibujo" es para poder explicarlo.
El lado de los puntos-comas, mide 32 codos.
La distancia en el suelo desde la base hasta la punta del bambú roto (asteriscos) mide 16.
Si llamamos x al trozo roto (guiones y comas, según si esta dibujado roto o sin romperse).
Podemos decir que 32-x, será el trozo que buscamos.
Hacemos las operaciones:
(32-x)²+16²=x²
Usamos las identidades notables para despejar el paréntesis.
32²-2x•32+x²+16²=x²
Hacemos los cuadrados y simplificamos las x² de cada lado de la igualdad.
1024-64x+256=0
64x=1024+256
x=1280/64
x=20
Como el trozo que buscábamos era 32-x, medirá 32-20=12 codos.
SOLUCIÓN: El trozo que se mantiene en pie mide 12 codos.
Lo que demuestra que soy mejor que mi hermano, jajajajaja.
Haber si llegamos los dos a la final, sería un puntazo!!
Un saludo!!
Luis!
Por cierto: he de decir que los problemas iban dirigidos a mi hermano (y al resto de personas que quieran, pero en especial a Ignacio) y que él también los está haciendo: aunque me halla adelantado yo, jejeje.
Respondo al de figuras imposibles:
Cuadrilátero de 2x3x6x12
Si ponemos de base 6 y le ponemos a cada uno de los extremos el de 2 y el de 3 con el máximo de abertura (en este caso 180, aunque ya sería el punto más extremo).
Se queda la base de 6, más 2 más 3 de cada lado, y como el angulo más extremo es 180, se suman (porque queda una linea recta) y el resultado es 6+3+2=11
Ya no podríamos ponerle de ninguna manera una linea de 12 arriba ya que se pasaría (esto con la abertura más extrema) y dado que no puede tener un ángulo de 180, si cerramos los angulos, aún se acorta más la distancia y más lejos se queda la recta de 12, de uno de los extremos de los lados.
El del triángulo, lo mismo.
Con un ángulo de 180, quedaría 3: base; 2: lado, al tener el ángulo de 180 se podrían sumar (porque formarían una sola recta) y el otro segmento mide 9, lo mismo que la base más el lado, y dado que no puede tener un angulo de 180, con que cerremos un poquito el ángulo, ya no podrían juntarse las tres líneas, por la misma razón que el cuadrado.
Ahora unas dudas de mi hermano y mias:
Al problema del loto le falta algún dato?
La arista del cuboctaedro son 10, sin haberle recortado a la mitad las aristas, o 10 con las aristas ya recortadas??
Un saludo!!!!
Hola
EL OCTAEDRO:
El volumen del octaedro es:
1/3 RAIZ CUADRADA(2)•a³
a= lado
1/3 RAIZ CUADRADA(2)•1000= 471.4045208 cm³
SOLUCIÓN:
El octaedro tiene 471.404 cm³ de volúmen
En un rato pongo el del cuboctaedro...
salu2
Ignacio
logicayestrategia.blogspot.com
jojojo. Voy a intentar corregirlos en un plis plas. Problema del bambú ok, problema de los cuadriláteros y triángulos imposibles, ok, problema del octaedro ok (aunque la fórmula del volumen del octaedro no te la iban a decir, la tendrías que deducir, y es que un octaedro está compuesto de 2 pirámides de base cuadrada, cuyas alturas son raíz de 50), el problema de la flor de loto os lo explico en el siguiente comentario, y estoy deseando que me mandeis resuelto el cuboctaedro... No tengo tiempo para poneros más problemas. Os deseo toda la suerte del mundo, dejad algo para mis alumnos, por fa... Es broma, que ganen los mejores, y yo personalmente os incluyo en ese grupo. Como me gustaría daros clase...
Cambiad la flor de loto por la espiga de un junco. Este junco cuando está vertical sobresale medio codo, pero si lo arrastras dos codos hacia un lado lo que sobresale desaparece, está todo el junco bajo el agua. Los juncos no se doblan. No falta ningún dato. Intentaré hacer el dibujo.
*
* ----->
|__________________
|.........*...........
|........* ...........
|......./.............
|....../..............
|...../...............
|..../................
|.../.................
|../..................
|./...................
|/....................
Por cierto, no voy a ir con mis alumnos, irá en mi lugar el otro profe de mates. Lo siento. En otra ocasión os conoceré... Suerte.
Madre mia que churro de dibujo el mio... será porque no reconoce los espacios y los borra...
El del junco:
No se si está bien... pero creo que si
Llamamos a la altura del junco x.
La profundidad del agua será x-0.5(el 0.5 es el que sobresale por encima del agua).
La distancia entre el junco vertical y el hundido es de 2 codos.
Por lo tanto podemos dibujar un triangulo cuadrado si prescindimos de la parte que sobresale al estar por encima del agua.
Teorema de Pitagoras:
(x-0.5)²+2²=x²
(x-0-5) es la parte sumergida cuando está vertical.
x es la altura del junco
2 es la separación entre el junco vertical y el diagonal hundido.
Operamos:
x²-2x•0.5+0.5²+4=x²
-x+0.25+4=0
x=4.25
Tenemos la altura del junco.
Como sobresale 0.5 codos de la superficie, la profundidad será (altura junco)-(parte sobresaliente)=4.25-0.5=3'75 codos.
SOLUCIÓN: La profundidad del lago es de 3'75 codos.
Un saludo!!!
Correcto, Luis, ma;ana a por el cuboctaedro. Ahora nos vamos todos a dormir. hasta ma;ana
Menudo ajetreo trae Mamat el matemático por estos lares,tanta formula y tanta X por despejar... Buuu, menos mal que yo ya terminé con esas cosas, y aprobé y todo en esos Bonillos, todavía no me he encontrao en mi vida cotidiana ningún problema de estos, o quizá no haya estado atento. A ver si ganan tus alumnos tal competición, yo me quedo sorprendio, la verdad... que cocos! El ex-alumno Víctor. jaja
Hola Miguel...
me salio super bien la olimpiada xD
hice todos los problemas y yo creo que bien
y salió el del curioso 2009:
2009= 200•9+200+9
y me salió bastante bien
Enrique, ya me driás como te han salido
Suerte!!
salu2
Ignacio
y que paso con la solucion del cuboctaedro? nono necesito q me den una manito con eso!
Publicar un comentario